Простые криптосистемы

Криптографические методы являются наиболее эффективными средствами защиты информации в автоматизированных системах (АС). А при передаче информации по протяженным линиям связи они являются единственным реальным средством предотвращения несанкционированного доступа.

Основные требования к криптографическому закрытию информации в АС

1. Сложность и стойкость криптографического закрытия данных должны выбираться в зависимости от объема и степени секретности данных.
2. Надежность закрытия должна быть такой, чтобы секретность не нарушалась даже в том случае, когда злоумышленнику становится известен метод шифрования.
3. Метод закрытия, набор используемых ключей и механизм их распределения не должны быть слишком сложными.
4. Выполнение процедур прямого и обратного преобразований должно быть формальным. Эти процедуры не должны зависеть от длины сообщений.
5. Ошибки, возникающие в процессе преобразования не должны распространяться по системе.
6. Вносимая процедурами защиты избыточность должна быть минимальной.

Классификация основных методов криптографического закрытия информации

1. Шифрование
   1. Подстановка (замена)
      1. Одноалфавитная
      2. Многоалфавитная одноконтурная обыкновенная
      3. Многоалфавитная одноконтурная монофоническая
      4. Многоалфавитная многоконтурная
   2. Перестановка
      1. Простая
      2. Усложненная по таблице
      3. Усложненная по маршрутам
   3. Гаммирование
      1. С конечной короткой гаммой
      2. С конечной длинной гаммой
      3. С бесконечной гаммой
   4. Аналитические преобразования
      1. Матричные
      2. По особым зависимостям
   5. Комбинированные
      1. Подстановка+перестановка
      2. Подстановка+гаммирование
      3. Перестановка+гаммирование
      4. Гаммирование+гаммирование
2. Кодирование
   1. Смысловое
      1. По специальным таблицам
   1. Символьное
      1. По кодовому алфавиту
3. Другие виды
   1. Рассечение-разнесение
      1. Смысловое
      2. Механическое
   2. Сжатие-расширение

Начиная разговор о шифровании, определимся с терминологией на примере фильма "Семнадцать мгновений весны": Юстас - зашифровывает, Алекс - расшифровывает, а старина Мюллер - дешифрует сообщение.

Шифрование методом замены (подстановки)

Наиболее простой метод шифрования. Символы шифруемого текста заменяются другими символами, взятыми из одного алфавита (одноалфавитная замена) или нескольких алфавитов (многоалфавитная подстановка).

Одноалфавитная подстановка

Простейшая подстановка - прямая замена символов шифруемого сообщения другими буквами того же самого или другого алфавита.

Примеры таблиц замены:

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
М Л Д О Т В А Ч К Е Ж Х Щ Ф Ц Э Г Б Я Ъ Ш Ы З И Ь Н Ю У П С Р Й

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Q W E R T Y U I O P [ ] A S D F G H J K L Z X C V B N M < > @ %

Стойкость метода простой замены низкая. Зашифрованный текст имеет те же самые статистические характеристики, что и исходный, поэтому зная стандартные частоты появления символов в том языке, на котором написано сообщение, и подбирая по частотам появления символы в зашифрованном сообщении, можно восстановить таблицу замены. Для этого требуется лишь достаточно длинный зашифрованный текст, для того, чтобы получить достоверные оценки частот появления символов. Поэтому простую замену используют лишь в том случае, когда шифруемое сообщение достаточно коротко!

Стойкость метода равна 20 - 30, трудоемкость определяется поиском символа в таблице замены. Для снижения трудоемкости при шифровании таблица замены сортируется по шифруемым символам, а для расшифровки формируется таблица дешифрования, которая получается из таблицы замены сортировкой по заменяющим символам.

Многоалфавитная замена повышает стойкость шифра.

Многоалфавитная одноконтурная обыкновенная подстановка

Для замены символов используются несколько алфавитов, причем смена алфавитов проводится последовательно и циклически: первый символ заменяется на соответствующий символ первого алфавита, второй - из второго алфавита, и т.д. пока не будут исчерпаны все алфавиты. После этого использование алфавитов повторяется.

Рассмотрим шифрование с помощью таблицы Вижинера - квадратной матрицы с n² элементами, где n - число символов используемого алфавита. В первой строке матрицы содержится исходный алфавит, каждая следующая строка получается из предыдущей циклическим сдвигом влево на один символ.

Таблица Вижинера для русского алфавита:

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я
Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А
В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б
Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В
Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г
Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д
Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е
З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж
И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З
Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И
К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й
Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К
М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л
Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М
О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н
П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О
Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П
С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р
Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С
У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т
Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У
Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф
Ц Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х
Ч Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц
Ш Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч
Щ Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш
Ь Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ
Ы Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь
Ъ Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы
Э Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ
Ю Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э
Я А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю

Для шифрования необходимо задать ключ - слово с неповторяющимися символами. Таблицу замены получают следующим образом: строку "Символы шифруемого текста" формируют из первой строки матрицы Вижинера, а строки из раздела "Заменяющие символы" образуются из строк матрицы Вижинера, первые символы которых совпадают с символами ключевого слова.

При шифровании и дешифровании нет необходимости держать в памяти всю матрицу Вижинера, поскольку используя свойства циклического сдвига, можно легко вычислить любую строку матрицы по ее номеру и первой строке.

При шифровании символы из первой строки заменяются символами остальных строк по правилу

                a(1,i) -> a(k,i),

Используя свойства циклического сдвига влево элементы k-ой строки можно выразить через элементы первой строки

                          a(1,i+k-1), если i<=n-k+1
                a(k,i)=                               
                          a(1,i-n+k-1), если i>n-k+1

При дешифровании производится обратная замена

                a(k,i) -> a(1,i).

Поэтому необходимо решить следующую задачу: пусть очередной дешифруемый символ в тексте - a(1,j) и для дешифрования используется k-я строка матрицы Вижинера. Необходимо найти в k-ой строке номер элемента, равного a(1,j). Очевидно,

                          a(k,j-k+1), если j>=k
                a(1,j)=
                          a(k,n-k+j+1), если j<k

Таким образом при дешифровании по k-ой строке матрицы Вижинера символа из зашифрованного текста, значение которого равно a(1,j), проводится обратная подстановка

                          a(1,j-k+1), если j>=k
                a(1,j) ->
                          a(1,n-k+j+1), если j<k

Стойкость метода равна стойкости метода подстановки, умноженной на количество используемых при шифровании алфавитов, т.е. на длину ключевого слова и равна 20*L, где L - длина ключевого слова.

С целью повышения стойкости шифрования предлагаются следующие усовершенствования таблицы Вижинера:

1. Во всех (кроме первой) строках таблицы буквы располагаются в произвольном порядке.
2. В качестве ключа используются случайные последовательности чисел, которые задают номера используемых строк матрицы Вижинера для шифрования.

В монофонической подстановке количество и состав алфавитов выбирается таким образом, чтобы частоты появления всех символов в зашифрованном тексте были одинаковыми. При таком положении затрудняется криптоанализ зашифрованного текста с помощью его статистической обработки. Выравнивание частот появления символов достигается за счет того, что для часто встречающихся символов исходного текста предусматривается большее число заменяющих символов, чем для редко встречающихся.

Пример таблицы монофонической замены:

А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ь Ы Ъ Э Ю Я _
Ф Н ( Щ И Г Е R A Д Ы ~ @ S Л Я Ж ^ C Ш М Б Q П Т Х Ю Ъ Р } \ _ #
* Н У Щ D + Е R = Д Ц Й Ч [ В Ь ) O & { М Б Q П Т Х Ю Ъ Р } \ _ <
Л Н ( Щ И ] Е R % Д Ы ~ @ G / Я Э З " Ш М Б Q П Т Х Ю Ъ Р } \ _ W
Ф Н У Щ D К Е R A Д Ц Й Ч S + Ь Ж ^ C { М Б Q П Т Х Ю Ъ Р } \ _ V

Шифрование проводится так же, как и при простой подстановке, с той лишь разницей, что после шифрования каждого символа соответствующий ему столбец алфавитов циклически сдвигается вверх на одну позицию. Таким образом, столбцы алфавитов как бы образуют независимые друг от друга кольца, поворачиваемые вверх на один знак каждый раз после шифрования соответствующего знака исходного текста.

Многоалфавитная многоконтурная подстановка

Многоконтурная подстановка заключается в том, что для шифрования используются несколько наборов (контуров) алфавитов, используемых циклически, причем каждый контур в общем случае имеет свой индивидуальный период применения. Частным случаем многоконтурной полиалфавитной подстановки является замена по таблице Вижинера, если для шифрования используется несколько ключей, каждый из которых имеет свой период применения.

Общая модель шифрования подстановкой может быть представлена в следующем виде:

Если w фиксировано, то формула описывает одноалфавитную подстановку, если w выбирается из последовательности w₁ ,w₂ ,...,w_n, то получается многоалфавитная подстановка с периодом n.

Если в многоалфавитной подстановке n > m (где m - число знаков шифруемого текста) и любая последовательность w_i, i=1,2,...,n используется только один раз, то такой шифр является теоретически нераскрываемым. Такой шифр получил название шифра Вермэна.

Стойкость простой многоалфавитной подстановки оценивается величиной 20*n, где n - число различных алфавитов, используемых для замены. Усложнение многоалфавитной подстановки существенно повышает ее стойкость. Монофоническая подстановка может быть весьма стойкой (и даже теоретически нераскрываемой), однако строго монофоническую подстановку реализовать на практике трудно, а любые отклонения от монофоничности снижают реальную стойкость шифра.

Шифрование методом перестановки

При шифровании перестановкой символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока этого текста.

Простая перестановка

Выбирается размер блока шифрования в n столбцов и m строк и ключевая последовательность, которая формируется из натурального ряда чисел 1,2,...,n случайной перестановкой.

Шифрование проводится в следующем порядке:

1. Шифруемый текст записывается последовательными строками под числами ключевой последовательности, образуя блок шифрования размером n*m.
2. Зашифрованный текст выписывается колонками в порядке возрастания номеров колонок, задаваемых ключевой последовательностью.
3. Заполняется новый блок и т.д.

Например, зашифруем текст

блоком размером 8*3 и ключом 5-8-1-3-7-4-6-2.

Таблица простой перестановки будет иметь вид:

			   Ключ
5	8	1	3	7	4	6	2

Г	Р	У	З	И	Т	Е	_
А	П	Е	Л	Ь	С	И	Н
Ы	_	Б	О	Ч	К	А	Х

Зашифрованное сообщение:

Расшифрование выполняется в следующем порядке:

1. Из зашифрованного текста выделяется блок символов размером n*m.
2. Этот блок разбивается на n групп по m символов.
3. Символы записываются в те столбцы таблицы перестановки, номера которых совпадают с номерами групп в блоке. Расшифрованный текст читается по строкам таблицы перестановки.
4. Выделяется новый блок символов и т.д.

При усложнении перестановки по таблицам для повышения стойкости шифра в таблицу перестановки вводятся неиспользуемые клетки таблицы. Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования.

При шифровании текста в неиспользуемые элементы не заносятся символы текста и в зашифрованный текст из них не записываются никакие символы - они просто пропускаются. При расшифровке символы зашифрованного текста также не заносятся в неиспользуемые элементы.

Для дальнейшего увеличения криптостойкости шифра можно в процессе шифрования менять ключи, размеры таблицы перестановки, количество и расположение неиспользуемых элементов по некоторому алгоритму, причем этот алгоритм становится дополнительным ключом шифра.

Перестановка, усложненная по маршрутам

Высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используются несколько различных маршрутов. Для примера рассмотрим шифрование по маршрутам Гамильтона при n=3.

Струкрура трехмерного гиперкуба:

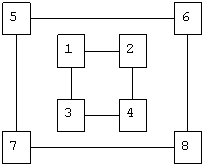
Номера вершин куба определяют последовательность его заполнения символами шифруемого текста при формировании блока. В общем случае n-мерный гиперкуб имеет n² вершин.

Маршруты Гамильтона имеют вид:

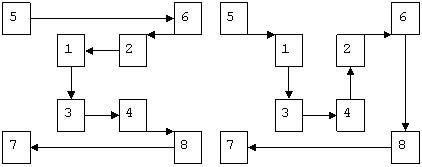
Последовательность перестановок символов в шифруемом блоке для первой схемы 5-6-2-1-3-4-8-7, а для второй 5-1-3-4-2-6-8-7. Аналогично можно получить последовательность перестановок для других маршрутов: 5-7-3-1-2-6-8-4, 5-6-8-7-3-1-2-4, 5-1-2-4-3-7-8-6 и т.д.

Размерность гиперкуба, количество вид выбираемых маршрутов Гамильтона составляют секретный ключ метода.

Стойкость простой перестановки однозначно определяется размерами используемой матрицы перестановки. Например, при использовании матрицы 16*16 число возможных перестановок достигает 1.4E26. Такое число вариантов невозможно перебрать даже с использованием ЭВМ. Стойкость усложненных перестановок еще выше. Однако следует иметь в виду, что при шифровании перестановкой полностью сохраняются вероятностные характеристики исходного текста, что облегчает криптоанализ.

Шифрование методом гаммирования

Суть метода состоит в том, что символы шифруемого текста последовательно складываются с символами некоторой специальной последовательности, называемой гаммой. Иногда такой метод представляют как наложение гаммы на исходный текст, поэтому он получил название "гаммирование".

Наложение гаммы можно осуществить несколькими способами, например по формуле

Расшифрование текста проводится по той же формуле:

Последовательность гаммы удобно формировать с помощью датчика псевдослучайных чисел (ПСЧ).

Стойкость гаммирования однозначно определяется длиной периода гаммы. При использовании современных ПСЧ реальным становится использование бесконечной гаммы, что приводит к бесконечной теоретической стойкости зашифрованного текста.

Шифрование с помощью аналитических преобразований

Достаточно надежное закрытие информации может обеспечить использование при шифровании некоторых аналитических преобразований. Например, можно использовать методы алгебры матриц - в частности умножение матрицы на вектор.

В качестве ключа задается квадратная матрица ||a|| размера n*n. Исходный текст разбивается на блоки длиной n символов. Каждый блок рассматривается как n-мерный вектор. А процесс шифрования блока заключается в получении нового n-мерного вектора (зашифрованного блока) как результата умножения матрицы ||a|| на исходный вектор.

Расшифрование текста происходит с помощью такого же преобразования, только с помощью матрицы, обратной ||a||. Очевидно, что ключевая матрица ||a|| должна быть невырожденной.

Комбинированные методы шифрования

Достаточно эффективным средством повышения стойкости шифрования является комбинированное использование нескольких различных способов шифрования, т.е. последовательное шифрование исходного текста с помощью двух или более методов.

Стойкость комбинированного шифрования S не ниже произведения стойкостей используемых способов

Если какой-либо способ шифрования при независимом применении может обеспечить стойкость не ниже S, то комбинировать его с другими способами целесообразно лишь при выполнении условия

Организационные проблемы криптозащиты

Рассмотренные значения стойкости шифров являются потенциальными величинами. Они могут быть реализованы при строгом соблюдении правил использования криптографических средств защиты.

Основные правила криптозащиты:

1. Сохранение в тайне ключей.
2. Исключение дублирования.
3. Достаточно частая смена ключей.

Под дублированием здесь понимается повторное шифрование одного и того же отрывка текста с использованием тех же ключей (например, если при первом шифровании произошел сбой). Нарушение этого правила резко снижает надежность шифрования, так как исходный текст может быть восстановлен с помощью статистического анализа двух вариантов зашифрованного текста.

Важнейшим правилом криптозащиты является достаточно частая смена ключей. Причем частота может определяться исходя из длительности использования ключа или исходя из объема зашифрованного текста. При этом смена ключей по временному графику является защитной мерой против возможного их хищения, смена после шифрования определенного объема текста - от раскрытия шифра статистическими методами.

Нельзя допускать злоумышленнику возможности направить в систему ряд специально подобранных сообщений и получать их в зашифрованном виде. Такого взлома не может выдержать ни одна криптосистема!

Важными аспектами организации криптозащиты являются выбор способа закрытия, распределение ключей и доставка их в места пользования (механизм распределения ключей).

Выбор способа защиты тесно связан с трудоемкостью метода шифрования, степенью секретности закрываемых данных, стойкостью метода и объемом шифруемой информации.

Один из принципов криптографии является предположение о несекретности метода закрытия информации. Предполагается, что необходимая надежность закрытия обеспечивается только за счет сохранения в тайне ключей. Отсюда вытекает принципиальная важность формирования ключей, распределения их и доставка в пункты назначения. Основными правилами механизма распределения ключей являются:

1. Ключи должны выбираться случайно.
2. Выбранные ключи должны распределяться таким образом, чтобы не было закономерностей в изменении ключей от пользователя к пользователю.
3. Должна быть обеспечена тайна ключей на всех этапах функционирования системы. Ключи должны передаваться по линиям связи, почте или курьерами в зашифрованном виде с помощью другого ключа. На практике часто образуется иерархия ключей шифрования, в которой ключи нижнего уровня при пересылке шифруются с помощью ключей верхнего уровня. Ключ в вершине иерархии не шифруется, а задается и хранится у доверенного лица, рассылается пользователям курьерами. Чем ниже уровень ключа, тем чаще он меняется и рассылается по линиям связи. Подобная схема шифрования ключей часто используется в сетях.

Литература 

1. Герасименко В.А., Размахнин М.К. "Криптографические методы в автоматизированных системах" Зарубежная радиоэлектроника,1982,N8
2. Сяо Д., Керр Д., С.Мэдник "Защита ЭВМ",М.,Мир,1982 - рассмотрены практически все аспекты защиты информации в вычислительных и автоматизированных системах.
3. Хоффман Л.Дж. Современные методы защиты информации. М.,Сов.радио, 1980 - наиболее полная и серьезная монография по теории и практике защиты информации
4. Джефф П.Р. Электроника,1973,т.46,N1 - шифрование данных методом гаммирования.
5. Уолкер Б.Дж., Блейк Я.Ф. Безопасность ЭВМ и организация их защиты.-М.:Связь,1980 - рассматриваются криптографические методы защиты информации, защита данных в файлах или базах данных.
6. Мануильямс Ф.Ж.,Слоан Н.Дж. ТИИЭР,1976,т.64,N12 - детально описаны способы формирования и свойства псевдослучайных последовательностей, которые используются при шифровании данных методом гаммирования.